1. CPG based control with minimal feedback:

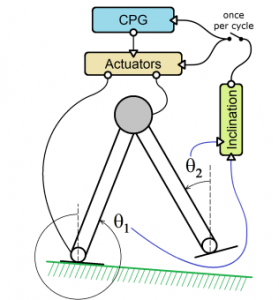
Our research focuses on controlling legged robots using natural dynamics. The basic approach, depicted in Figure 1 for the control of the biped robot, is based on the biomimetic notion of central-pattern generator (CPG), which in our implementation generates torque signals as a function of its phase, and minimal feedback that changes the amplitude of these signals and the CPG. Generating torque pulses rather than joint trajectories allows the robot to exploits it natural dynamics, and the minimal feedback reduces sensory requirements. We have previously demonstrated the ability of this system to walk stably over a wide range of slopes (-8 to +7 degrees) (US Patent No. 20.140.031.986).

Figure 1: Compass biped controller. The compass biped includes two legs joined at the hip, torque actuators at ankle and hip, a central pattern generator (CPG) that generates the oscillatory phase, and legs’ inertial measurement units (IMUs) used to determine the inclination of the slope when both legs are on the ground.

 

2. Multi-objective optimization for optimizing controller parameters.

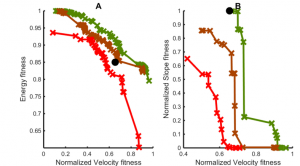
The parameters of the minimal feedback CPG-based controller (Figure 1) were optimized using Genetic Algorithm.  Different families of solutions emerged that excel in different aspects of the performance (Figure 1, right), including walking on varying terrain and speed (Spitz, Evstrachin, and Zacksenhouse, 2015 [1]).

Figure 2: Representative Pareto fronts generated by the multi-objective genetic algorithm (MOGA, right [Spitz et al, 2015]. Three-representative Pareto fronts are projected on two planes defined by the energy efficiency and velocity (A) and by robustness to slope variations and velocity (B).

 

3. Mono-pedal scooter robot

Mono-pedal scooter robot with series elastic actuation to enhance natural dynamics, walks successfully (Figure 2).

[youtube_sc url=”https://youtu.be/QTGFJt1m2Uo” title=”Mono-pedal%20scooter%20robot” color=”white” autohide=”0″]

Figure 3: Mono-pedal scooter robot with series-elastic actuators for implementing the natural dynamic controller. Middle: frontal view with cord connected to the external power supply, Right: side view with power supply on the cart, and close-up view in the insert showing the series elastic actuator.

 

4. Analytic stability analysis

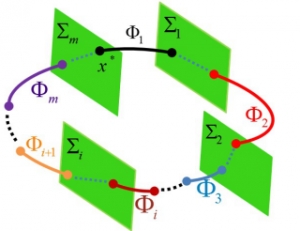
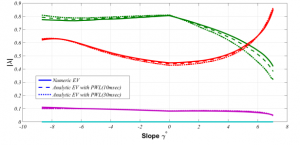
The dynamics of the walking robot can be modeled as an Hybrid dynamical system with (Figure 4, left) with continuous dynamics interrupted by discontinuous changes upon impact with the ground and changes in applied torque pulses. The eigenvalues of the linearized Poincare map were computed using the reduced Saltation Matrix [3] and agree well with the numerically computed eigenvalues (Figure 3, right). The robot is stable as long as the absolute values of the eigenvalues of the linearized Poincare map are below 1.

Figure 4: Analytic versus numeric stability analysis. Left: The dynamics of the robot controlled with the CPG-based controller was modeled as a hybrid dynamical system with multiple discontinuities (due to the impact with the ground and the torque pulses). Right: analytically computed eigenvalues (with piece-wise linear approximation) agree well with the numerically computed eigenvalues, and demonstrate stability over a wide range of sloped terrain.

 

5. Crab-walking strategy for walking on rough terrain

Control of a humanoid robot based on CPG that generates joint-trajectories. Its robust performance is depicted in the movie available on YouTube at https://www.youtube.com/watch?v=TQwOfpzHg7c and summarized in [4].

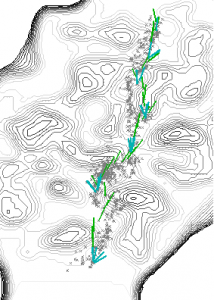
Figure 5: Crab walking. Top: pattern of movement during forward crawling and rotations. Right:  path traversed during the best trial is shown by green (forward step) and cyan (rotation) arrows, and the positions in all 10 trials are shown in points, superimposed on the height map of the hilly terrain.

 

6. Lateral stabilization

A decoupled controller that maintains the synchronization between the lateral and sagittal movements on a 3-dimensional compass biped with tail movements was developed. The control method successfully stabilizes the lateral movement as demonstrated and quantified by physical simulations with ADAMS. The simulated robot and example of stable limit cycles are shown in Figures 5. Further details are available in Yuval Shapira’s Master Thesis [5].

Figure 5: Tail movements for stabilization of 3-dimensional biped robot. Left: simulated 3-dimensional robot; Right: stable limit cycle.

7. Balancing robot walking with tail movements

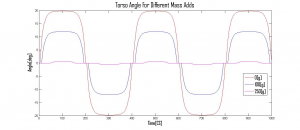
The Bioloid commercial bipedal robot was configured in the Dinosaur configuration (Figure 6, left) and modified to facilitate larger tail movements (Figure 6, right). Optimizing lateral tail movements, and increasing the tail mass, improved walking by reducing the movement of the torso (movie available). The project was conducted by two undergraduate students and detailed in [6].

Figure 6: Bioloid robot with tail for torso stabilization. The robot’s dinosaur configuration was extended to add a tail (left) which lateral movements reduced torso movements during walking (right).

 

Publications:

• [1] Spitz J., A. Evstrachin, and M. Zacksenhouse, Minimal feedback to a rhythm generator improves the robustness to slope variations of a compass biped, Bioinspiration & Biomimetics, 10(5), 056005, 2015.
• [2] Schallheim I. and M. Zacksenhouse, Integrating refleces with open loop central pattern generator increases robustness of scooter-gait, submitted to Int. Conf on Robotics and Automation, ICRA 2016.
• [3] Evstrachin A., Spitz J., Sidorov E., and M. Zacksenhouse, Analytic linearization of Poincare maps of hybrid systems and its application for simple hopping and walking robots. Submitted to SIAM Journal on Applied Dynamical Systems.
• [4] Spitz J., E. Sidorov, and M. Zacksenhouse, Humanoids can take advantage of crab-walking gaits, J. Humanoid Robots 12(2), 1550004:1-23, DOI: 10.1142/S0219843615500048, 2014.
• [5] Shapira Y., Dynamic and control of biologically inspired walking biped robot. Master Thesis, Faculty of Mechanical Engineering, Technion (under the supervision of M. Zacksenhouse).
• [6] Palmon and S. Rorberg, Robot stabilization with tail movements (Project report, 2015).